名古屋工業大学 原子核理論研究室

原子核とシェル構造

　原子核は、物質を構成する原子の中心にあって原子の質量の大半を担う、大きさ数フェムトメートル (1fm=10^-15 m) の粒子で、正の電荷をもつ陽子と電荷をもたない中性子とがほぼ同数個、核力という力により結合してできています。原子核の種類は陽子と中性子の数の組み合わせによって決まり、約300種の安定な原子核に加え、約3000種類の不安定な原子核（有限の寿命で崩壊して安定な原子核に変化するもの）の存在も確認されています。核子（原子核を構成する陽子と中性子の総称）は、それらを結び付ける強い束縛力とは裏腹に原子核内を比較的自由に動き回ることができ、原子核の平均的な性質は原子核を液体のしずくになぞらえた液滴模型 (liquid drop model) によりとてもよく記述することができます。さらに原子核の質量を構成核子数の関数として詳しくみると、液滴模型で記述される平均的な振舞いに加えて、規則的な揺らぎが存在することが分かります。この揺らぎは、原子内に束縛された電子のエネルギースペクトルに起因する原子の周期律と同様、原子核内に束縛された核子の運動を量子化したエネルギースペクトルの構造（シェル構造）に由来しています。核子エネルギーの固有値スペクトルは、固有値の近い準位が密集した「シェル」と準位がほとんどない「ギャップ」とが交互に現れる周期的な構造をもち、密集した準位群が完全に占有された閉殻 (closed shell) 構造において原子核は特に強い安定性を示します。これは原子の周期律表の右端の貴ガス元素に相当し、これに対応する粒子数 (2, 8, 20, 28, 50, 82, 126, …) のことを原子核分野では「魔法数」(magic number) と呼んでいます。原子では粒子の種類が電子のみですが、原子核には陽子と中性子の２種類の粒子があり、両者のシェル構造を考える必要があります。陽子数 Z が共通で中性子数 N の異なる原子核をアイソトープ（同位核）、中性子数 N が共通で陽子数 Z の異なる原子核をアイソトーン（同調核）と言います。同位核（同調核）どうしで比較すると中性子数（陽子数）が魔法数に一致するところで核子あたりの束縛エネルギーが極大になります。特に陽子数も中性子数も魔法数に一致するものを二重閉殻核と言い、酸素16 (N=Z=8), カルシウム40 (N=Z=20), スズ132(N=82, Z=50), 鉛208 (N=126, Z=82) などがこれにあたります。

原子核の変形

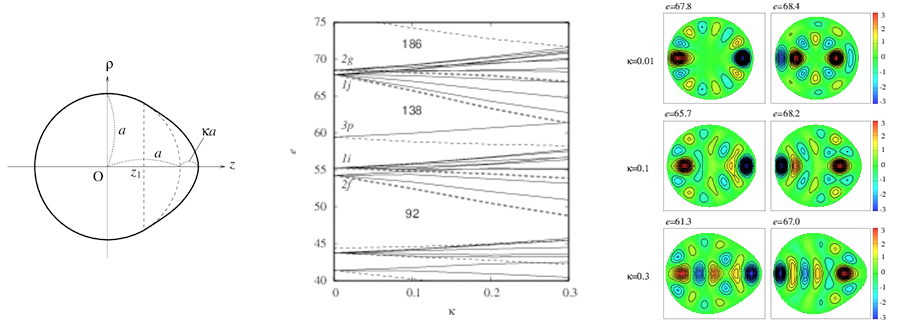
　核子運動を量子化したスペクトルのシェル構造は、閉殻構造を安定化させる、すなわち原子核のエネルギーを低くするのに対して、閉殻からはずれた構造に対してはエネルギー的に不利にはたらきます。液滴の表面張力により原子核は球形に近い形をしており、上で述べたシェル構造は球形の平均ポテンシャル中を運動する核子運動を量子化することにより生じたものです。このシェル構造は平均ポテンシャルの形に強く依存しており、原子核の形が変化するとシェル構造が大きく変化します。球形でシェル構造によりエネルギー的に不利な原子核は、変形によってシェル構造を変化させることによって、より低いエネルギーを実現できる場合があります。これが原子核の変形の主要な微視的メカニズムであると考えられています。魔法数からはずれた原子核は変形しており、その多くは四重極変形という、対称軸方向に伸びたラグビーボール型（レモン型）や対称軸方向に縮んだパンケーキ型（みかん型）の形状をしています。また、陽子数と核子数の組み合わせによっては、八重極変形という、軸対称な洋梨型や、正四面体型などの反転非対称な変形状態も実現されることが実験、理論の両面から示唆されています。原子番号92のウランより大きな原子核では、陽子間のクーロン斥力を核力でささえることができなくなり、核分裂を起こして小さな原子核になります。核分裂は原子核変形のもっとも顕著な形態ととらえることができます。液滴模型によると同じ大きさの２つの原子核に分裂する場合がエネルギー的に最も有利ですが、多くの原子核の核分裂は大きさの異なる原子核に分裂する「非対称分裂」であることが知られています。この分裂片の質量分布にも、シェル構造が重要な役割を果たしています。アクチノイドと呼ばれる原子番号Z=89~103の原子核の核分裂においては、重い分裂片の質量数 A=N+Z が140近辺に集中していますが、分裂過程で安定な二重閉殻のスズ132が形成されると考えることによりこれらの非対称分裂を説明することができます。原子核の変形は、原子核の性質をさぐるうえでの根幹をなしており、原子核構造研究の最も重要なテーマとなっています。

シェル構造の半古典的起源

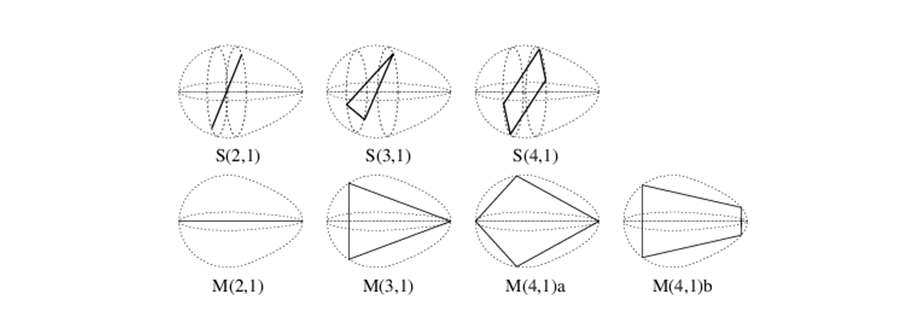
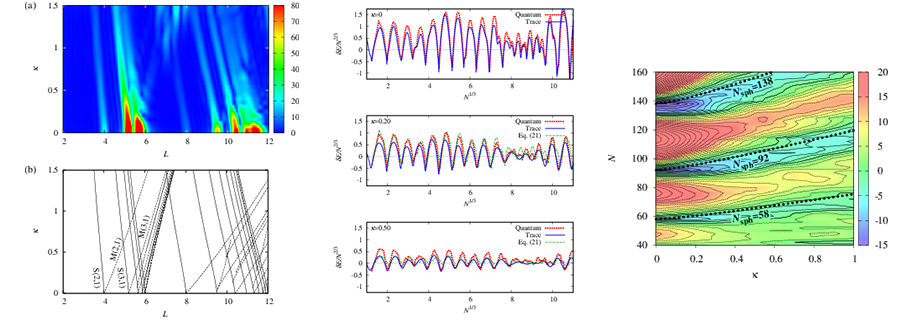
　一般に、ポテンシャルに束縛された粒子の量子力学的なエネルギースペクトルを計算すると、系によって程度の差はあれ、シェル構造、すなわち準位分布の規則的な揺らぎ構造が存在することが見てとれます。では、この規則的な構造の起源はどのように説明することができるでしょうか。エネルギー固有値が解析的に求められる特殊な場合を除いて、純粋に量子論的な概念でシェル構造を説明することは困難です。フランスの数理物理学者 R. Balian と C. Bloch は、球形無限井戸型ポテンシャルに閉じ込められた粒子のエネルギースペクトル（球ベッセル関数のゼロ点分布から得られる）の大局的構造が、2つの異なる振動数をもつ振動関数を重ね合わせてできるうなり構造をもつことを見出し、この振動数が井戸型ポテンシャル中を運動する古典的な粒子の周期軌道に関係していることを示しました。彼らは、無限井戸型ポテンシャルの量子論的な準位分布に対する多重反射展開の式を用い、これを半古典的に評価することにより、準位分布を古典周期軌道の寄与で表す公式を導いたのです。またこれとは独立に、スイスの M. Gutzwiller は、量子力学的な遷移振幅のファインマン経路積分表示を用い、これに半古典近似を適用することによって準位分布を古典周期軌道の寄与の和で表す「トレース公式」を導きました。これらにより、量子的な離散スペクトルがもつ大局的規則構造を、いくつかの短い古典周期軌道を用いて表すことができます。つまり、原子核変形の起源である変形ポテンシャル中の量子論的シェル構造を、主要な古典周期軌道の性質との対応から分析することができるのです。私たちの研究室では、このトレース公式およびその拡張理論にもとづくさまざまな核子数領域における原子核の変形やその系統性の解析を中心として、関連する原子核物理や量子多体系物理についての理論的研究を行っています。